Transmission Line Sag Calculation

Transmission line sag is a critical parameter in the design and operation of overhead power lines. It refers to the vertical distance between the lowest point of the conductor and an imaginary straight line drawn between the points of support. Accurate calculation of sag is essential to ensure the safety, reliability, and efficiency of the power transmission system. Here's a step-by-step guide on how to calculate transmission line sag:

Parameters Required

1. Span length (L): The horizontal distance between two support points (towers or poles).
2. Conductor weight per unit length (w): This includes the weight of the conductor itself and any additional load due to ice, wind, etc.
3. Tension in the conductor (T): The horizontal tension in the conductor at the lowest point.
4. Conductor material properties: Such as the modulus of elasticity (E) and the coefficient of thermal expansion (α).
5. Temperature difference (ΔT): The difference between the installation temperature and the operating temperature.

Basic Formula

The basic formula for calculating the sag (S) of a conductor in a simple parabolic approximation is:

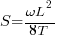
This formula assumes a uniform load distribution and horizontal tension in the conductor.

Steps for Calculation

Calculate the weight per unit length (w):

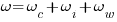
where
ω_c is the weight of the conductor,
ω_i is the additional weight due to ice, and
ω_w is the additional weight due to wind.

Determine the span length (L):
Measure the distance between the two support points.

Determine the tension (T):
The tension can be calculated or obtained from the manufacturer's data, considering factors like temperature, initial tension, and loading conditions.

Calculate the sag (S):
Using the basic sag formula:

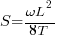
Example Calculation

Given:
Span length, L=300 meters
Conductor weight per unit length, ω=1.5 kg/m (including conductor, ice, and wind)
Tension in the conductor, T=5000 kg

Convert units if necessary:
Convert weight to Newtons (since 1 kg = 9.81 N):
ω = 1.5 × 9.81 = 14.715 N/m

Tension in Newtons:
T = 5000 × 9.81 = 49050 N

Calculate the sag:

Additional Considerations

Temperature Effects:

• If temperature effects are significant, adjust the tension accordingly.
• The tension can be adjusted for temperature using:
  
  where
  T₀ is the initial tension,
  T₁​ is the operating temperature, and
  α is the coefficient of thermal expansion.
• Elastic Stretching:

  Consider the elastic stretching of the conductor using the modulus of elasticity (E) and cross-sectional area (A):
  

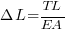
• Non-uniform Loads:

  For non-uniform loads or complex terrain, use more detailed analysis methods, such as the catenary equation.

Conclusion

The sag calculation is fundamental to ensuring that the conductor does not come too close to the ground or other structures, which could pose safety hazards. The basic formula provides a good approximation, but adjustments for temperature, elasticity, and non-uniform loading conditions may be necessary for more accurate results.