Heat dissipation in sealed electrical enclosures is a critical consideration in the design and operation of electrical or electronic systems. Effective heat management ensures the reliability, performance, and longevity of the components inside the enclosure.
Key aspects and methods to consider
- 1. Heat Generation
- Electronic components generate heat during operation. The amount of heat depends on the power consumption and efficiency of the components.
- 2. Thermal Conductivity
- Materials used in the enclosure and thermal interface materials affect how heat is conducted away from the components.
- 3. Ambient Temperature
- The temperature of the environment surrounding the enclosure influences the overall heat dissipation.
- 4. Thermal Resistance
This is the opposition to heat flow within the enclosure and between the enclosure and the environment.
Monitoring and Control
Managing heat dissipation in sealed electrical enclosures requires a combination of design strategies, material selection, and active or passive cooling methods. Careful consideration of these factors helps maintain the performance and reliability of electronic systems in various applications.
Place temperature sensors at critical points to monitor temperatures and ensure they remain within safe limits and implement control systems that adjust cooling methods dynamically based on temperature readings.
Calculation of Heat Dissipation in Sealed Electrical Enclosures
Calculating heat dissipation in sealed electrical enclosures involves understanding the thermal dynamics of the system and applying principles of heat transfer. Here are the steps to calculate heat dissipation:
1. Define the Parameters
- Heat Generation (Q). Total power dissipation of all components inside the enclosure, typically measured in watts (W).
- Enclosure Surface Area (A). The total external surface area of the enclosure through which heat can be dissipated, in square meters (m²).
- Thermal Conductivity of Enclosure Material (k). Measure of the material's ability to conduct heat, in watts per meter per degree Celsius (W/m·°C).
- Ambient Temperature (T_ambient). Temperature of the environment outside the enclosure, in degrees Celsius (°C).
- Internal Temperature (T_internal). Desired or measured temperature inside the enclosure, in degrees Celsius (°C).
- Thermal Resistance (R). The resistance to heat flow from the inside to the outside of the enclosure, in degrees Celsius per watt (°C/W).
2. Calculate Thermal Resistance
Thermal resistance is a key factor in determining how effectively heat can be dissipated from the enclosure. For a sealed enclosure, the thermal resistance can be broken down into two main components: conduction through the enclosure walls and convection from the exterior surface to the ambient air.
a. Conduction through Enclosure Walls
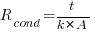
Where:
t = thickness of the enclosure walls (m)
k = thermal conductivity of the enclosure material (W/m·°C)
A = surface area of the enclosure (m²)
b. Convection from Enclosure Surface
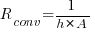
Where:
h = convective heat transfer coefficient (W/m²·°C)
A = surface area of the enclosure (m²)
The total thermal resistance is the sum of these resistances:
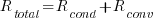
3. Determine the Heat Dissipation (Q)
Using the total thermal resistance, we can calculate the heat dissipation required to maintain a specific internal temperature:

4. Sample Calculation
Given Data:
Heat generation (Q): 100 W
Enclosure surface area (A): 1 m²
Thermal conductivity (k): 200 W/m·°C (for aluminum)
Wall thickness (t): 0.005 m
Convective heat transfer coefficient (h): 10 W/m²·°C
Ambient temperature (Tambient): 25°C
Desired internal temperature (Tinternal): 45°C
Calculate Thermal Resistance
Conduction Resistance
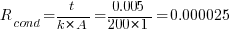 oC/W
oC/W
Convection Resistance
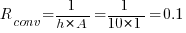 oC/W
oC/W
Total Thermal Resistance
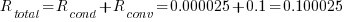 oC/W
oC/W
Determine Heat Dissipation
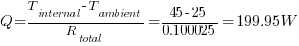
Thus, the enclosure needs to dissipate approximately 200 W to maintain an internal temperature of 45°C given the specified parameters.
