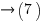This article will illustrate the basic theory of calculating a utility source impedance from fault data provided by power providers. Utility fault levels are usually expressed in MVA or Amperes (A).
I. Calculating source impedance from fault level expressed in Amperes (A)
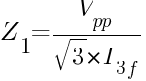

For sources other than power stations, Z2 can be taken as equal to Z1.
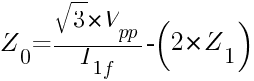
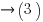
where:
Z1 = positive sequence impedance of source (ohm)
Z2 = negative sequence impedance of source (ohm)
Z0 = zero sequence impedance of source (ohm)
Vpp = phase-to-phase voltage, V
I3f = 3 phase fault current, A
I1f = phase-to-earth fault current, A
II. Calculating source impedance from fault level expressed in MVA
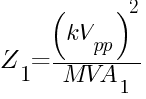
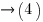
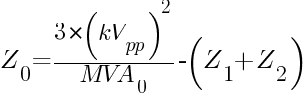
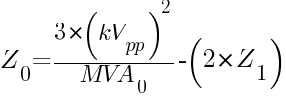
where:
kVpp = phase-to-phase voltage, kV
MVA1 = fault level on a 3-phase base, MVA
MVA0 = single phase-to-earth fault on a 3-phase base, MVA
When the impedance is given in % rather than in ohms