Capacitors are intended to solve problems, but if not properly specified, they can also create new ones.
Industrial and commercial customers are always examining their monthly electrical usage for cost-saving opportunities. Installing power factor correction capacitors can help reduce penalties imposed by utilities, often leading to a quick return on investment. In locations like hospitals and paper mills, the payback period for these capacitors can be as short as four to six months.
However, it's important not to install power factor correction capacitors without fully understanding their impact on the system. Non-linear loads, such as variable frequency drives (VFDs) for motors, DC power supplies for computers, and electronic ballasts for fluorescent lighting, generate harmonics. Failing to account for these harmonics and the system's inductive reactance can create the risk of harmonic resonance.
Harmonic Resonance
Harmonics are voltage or current distortions that occur at multiples of the fundamental frequency of an electrical system (50 Hz or 60 Hz, depending on the country). Harmonic frequencies can be generated by nonlinear loads like variable frequency drives (VFDs), rectifiers, and certain types of power electronics.
Harmonic Resonance occurs when the inductance and capacitance in a power system resonate at one of these harmonic frequencies, amplifying the distortion. Harmonic Resonance is a risk when capacitors interact with system inductances at harmonic frequencies, which can lead to system instability and damage. Careful design, including harmonic filtering or detuning, is crucial to prevent resonance.
Parallel Resonance
The operation of non-linear loads in a power distribution system creates harmonic currents that flow throughout the power system. The inductive reactance of that power system increases and the capacitive reactance decreases as the frequency increases, or as the harmonic order increases.
At a given harmonic frequency in any system where a capacitor exists, there will be a crossover point where the inductive and capacitive reactances are equal. This crossover point, called the parallel resonant point, is where the power system has coincidental similarity of system impedances. Every system with a capacitor has a parallel resonant point.
Parallel resonance causes problems only if a source of harmonics exists at the frequency where the impedances match. This is typically called harmonic resonance. Harmonic resonance results in very high harmonic currents and voltages at the resonant frequency. It’s extremely unlikely that these two impedances are exactly identical, but near resonance can be very damaging as well.
The formula for the parallel resonant frequency harmonic order:

where:
hR = parallel resonant frequency harmonic order
MVASC = source impedance in MVA
MVARCAP = 3-phase rating of capacitor in MVAR
Example:
MVASC = 500 MVA
MVARCAP = 10 MVAR
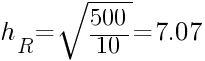
Hence a 10 MVAR capacitor bank will be resonant with the source impedance at the 7th harmonic order. That is 350Hz for 50Hz system or 420Hz for 60Hz system.
If any magnitude of 7th order harmonic current flows in the power system at that point where the capacitor bank is connected, the effect could be catastrophic.
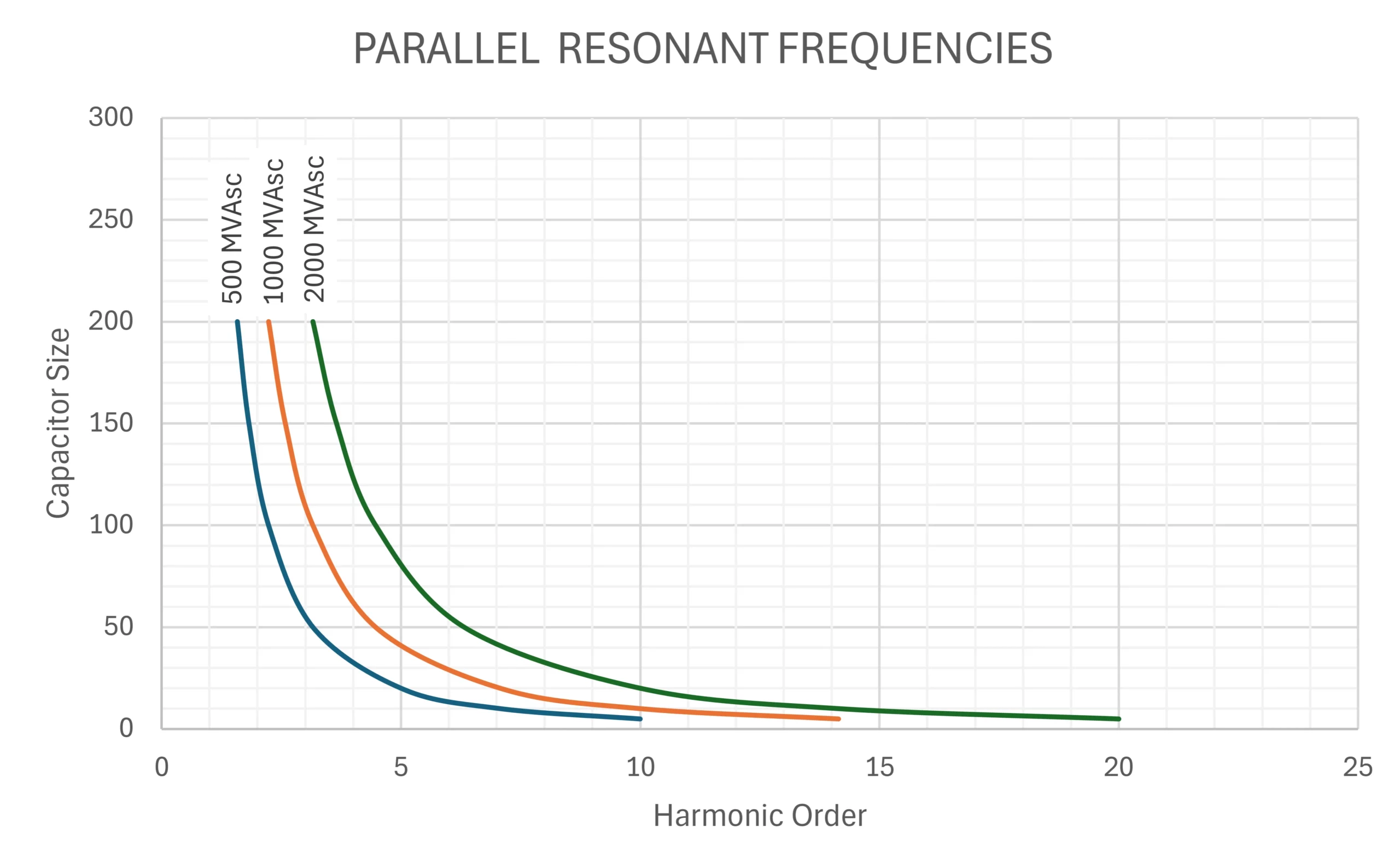
Below is a typical graph of the formula above.
How Harmonic Resonance Relates to Power Factor Correction
When capacitors are added for power factor correction, they introduce capacitance into the system. Combined with the inductive elements already present (e.g., transformers, motors), this creates the potential for resonance. If the natural resonant frequency of the LC circuit (inductor-capacitor circuit) matches or is close to a harmonic frequency, it can lead to significant resonance problems.
Ways to Mitigate Harmonic Resonance
1. Harmonic filters installed to prevent specific harmonic frequencies from building up in the system.
2. Detuned reactors which a basically inductors added in series with power factor correction capacitors to shift the resonant frequency away from the dominant harmonic frequencies.
3. Active power filters dynamically inject counter-harmonic frequencies to cancel out harmonics.
