After presenting the equations that we will be using for the Complex MVA Method in Part 1, we shall be learning how to combine MVAs or KVAs in this part.

In this tutorial,I have presented the methodology of combining KVAs. This principle will still be used for the Complex MVA Method.

I. Parallel MVAs

{MVA_total}={MVA_1}+{MVA_2}+{MVA_3}+...{MVA_n}

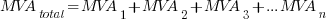
II. Parallel MVARs

{MVAR_total}={MVAR_1}+{MVAR_2}+{MVAR_3}+...{MVAR_n}

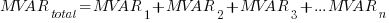
III. Parallel MWs

{MW_total}={MW_1}+{MW_2}+{MW_3}+...{MW_n}

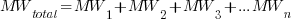
Example:

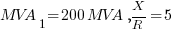{{MVA_1}=200MVA}, {{X/R}=5} is connected in parallel with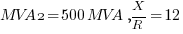 {{MVA2}=500MVA}, {{X/R}=12}

Using the equations in Part 1:

{MVA_1} = 200 MVA

{theta_1} = {tan^-1}{5} = 78.7^o

{MW_1} = {MVA_1}*cos {theta_1} = 39.2

{MVAR_1} = {MVA_1}*sin {theta_1} = 196.1

{MVA_2} = 500 MVA

{theta_2} = {tan^-1}(12) = 85.2^o

{MW_2} = {MVA_2}*cos {theta_2} = 41.8

{MVAR_2} = {MVA_2}*sin {theta_2} = 498.2

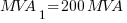
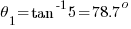
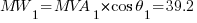
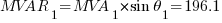
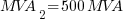
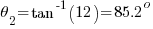
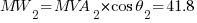
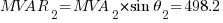
The resulting values will be:

MVA_total = 200+500 = 700

{MW_total} = 39.2+41.8 = 81

{MVAR_total} = 196.1+498.2 = 694.3

{X/R}_total = {694.3/81} = 8.6

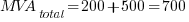
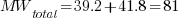
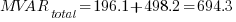
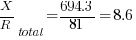
On the next part, we will be dealing with Complex MVA Method for MVAs in series.