Calculations:Per Unit System

Calculations:Per Unit System

Introduction

Single Line Diagram

The per-unit system is a method of expressing quantities in an electrical system (e.g. voltage, current, impedance, etc) as a proportion of pre-defined base quantities. By definition, the per-unit value of a quantity is the ratio of the original quantity to its base value (which results in a dimensionless "per-unit" or "pu" value):

$Q_{pu}={\frac {Q}{Q_{base}}}\,$

Where $Q_{pu}\,$ is the per-unit quantity (dimensionless or just "pu")

$Q\,$ is quantity in normal units

$Q_{base}\,$ is the base value of the quantity in normal units

For example, suppose the base value of current is 100A, then a current of 50A has a per-unit value of 50/100 = 0.5 pu.

Why bother?

The per-unit system was originally developed to simplify laborious hand calculations and while it is now not always necessary (due to the widespread use of computers), the per-unit system does still offer some distinct advantages over standard SI values:

• The relative magnitudes of all similar network quantities (e.g. voltages throughout the system) can be directly compared
• Constant terms such as ${\sqrt {3}}$ terms can be eliminated, and therefore avoids confusion between quantities (e.g. line-line vs line-neutral)
• Per-unit impedance values of equipment are normally found over a small range of values irrespective of the absolute size. On the other hand, ohmic values may have significant variation and are often proportional to nominal rating. Therefore, typical values can be used as a reasonable first approximation where detailed / accurate information is not known.
• Per-unit impedances of transformers are the same whether referred to either side of the transformer (primary or secondary) and are independent of winding connections (for polyphase transformers), voltage level and phase shifts
• Impedances are often quoted in terms of per-unit values by manufacturers (on a base of rated kVA or kW and voltage)
• Multiplying per-unit quantities results in more per-unit quantities (and requires no conversion of units)
• Manual calculations are often simplified using per-unit values (for all of the reasons above)

Calculation of Base Values

Not all system quantities are independent from each other (e.g. apparent power is related to voltage and current, S = VI), so base values are both selected and calculated. Normally, the rated (apparent) power and nominal voltage are arbitrarily selected as base quantities:

• Base power ($S_{base}\,$) = nominal apparent power of the equipment (or system)
• Base voltage ($V_{base}\,$) = nominal voltage of the equipment (or system)

The other base quantities can then be derived by calculation from these two base quantities:

Base current ($I_{base}={\frac {S_{base}}{V_{base}}}\,$)

(Note that for three-phase systems and where the base voltage is expressed as a line-to-line voltage, then $I_{base}={\frac {S_{base}}{{\sqrt {3}}V_{base}}}\,$)

Base impedance ($Z_{base}={\frac {V_{base}}{I_{base}}}={\frac {V_{base}^{2}}{S_{base}}}\,$)

(Note that for three-phase systems, $Z_{base}={\frac {V_{base,LN}}{I_{base}}}={\frac {V_{base,LL}^{2}}{S_{base}}}\,$, where $V_{base,LN}\,$ and $V_{base,LL}\,$ are the line-to-neutral and line-to-line base voltages respectively.

Base flux linkage ($\lambda _{base}={\frac {{\sqrt {2}}V_{rms,base}}{2\pi f_{base}}}\,$)

Calculation of Per-unit Impedances

Per-unit impedances are calculated by dividing the ohmic impedance by the base impedance:

$Z_{pu}={\frac {Z}{Z_{base}}}\,$

Per-unit resistance and reactance values can be calculated by dividing by the base impedance (which also works in series and parallel combinations of impedances), i.e.

$Z_{pu}={\frac {1}{Z_{base}}}\left(R+jX\right)\,$

Application Examples

System Analysis

The analysis of an electrical network can be simplified by using the per-unit system. Firstly, a system-wide base MVA is chosen and base voltages are selected for different parts of the system such that they correspond to the turns ratios of the transformers in the system. Choosing such voltages ensures that the per-unit impedance of the transformer is the same on both the primary and secondary sides and therefore the entire system can be combined using a single set of per-unit impedances. Next, all impedances in the network must be converted to the base values. Often, the per-unit impedance of system components are expressed on another base (e.g. transformer impedances are typically expressed on the rated kVA base and rated voltage). Therefore, we would need to perform a change of base operation:

$Z_{pu,new}=Z_{pu,old}\left({\frac {V_{old}}{V_{new}}}\right)^{2}\left({\frac {S_{new}}{S_{old}}}\right)\,$

Where $V_{old}\,$ and $V_{new}\,$ are the old and new base voltages (V)

$S_{old}\,$ and $S_{new}\,$ are the old and new base powers (VA)

Transformers

The transformer (leakage) impedance is normally expressed as a per-unit or percent quantity on the transformer kVA base and rated voltage. The impedance is calculated by computing the impedance voltage from a standard short-circuit test measurement - with the windings connected for the rated voltage (e.g. delta, wye, etc), a variable voltage is applied to one winding with the other winding short circuited. The impedance voltage is the value of the applied voltage required to circulate the rated current in the winding (that is not short circuited). The per-unit impedance of the transformer is found by converting the impedance voltage to a per-unit quantity.

$Z={\frac {V_{z}}{V_{base}}}\,$

Where $V_{z}\,$ is the impedance voltage (V)

$V_{base}\,$ is the transformer rated (base) voltage (V)

An advantage of the per-unit impedance is that it is the same whether it is referred to the primary or secondary side of the transformer and is independent of winding connection (e.g. delta, wye, etc) and phase shifts.

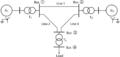
Induction Machines

It is often more convenient to express induction motor equivalent circuit parameters in per-unit since they are invariant of winding connection. First, select the power and voltage base values as the nominal kVA rating and the rated voltage of the induction motor. The motor full load current is therefore the current base. The other per-unit quantities can be calculated as follows:

• Rated active power (pu): $P_{fl}=\cos \phi _{fl}\,$
• Rated reactive power (pu): $Q_{fl}=\sin \phi _{fl}\,$
• Rated mechanical power (pu): $P_{m,fl}=\cos \phi _{fl}\eta \,$
• Rated torque (pu): $T_{fl}={\frac {\cos \phi _{fl}\eta }{1-s_{f}}}\,$